Introduction
In this essay, I introduce the concept of functional equality, and discuss why 2+2 may or may not equal 4.0.
Obviously 2+2 is mathematically equal to 4.0. And yet in many programming languages, the integer and float representations of the same number are functionally different values, because operations such as division and conversion-to-string behave differently for different types.
When comparing two values for equality, it is important to ask, what do you mean by “equal”? In some cases, programmers just want to know if two values represent the same ideal value, such as the same point on the number line, the same moment in time, or the same physical quantity.
But in other cases, what matters is whether the two values are, for all intents and purposes, exchangeable in code: you can replace one value with the other in your program and get the exact same output. This only happens if the two values are functionally equal.
In this essay I will explore the difference between functional equality and ideal equality. Both types of equality comparisons are sometimes necessary, and this gives rise to what I call the expression problem. I explore how some common programming languages solve the expression problem by supporting different ways of doing equality comparisons. I argue that the == operator should always respect functional equality, and that ideal equality tests should be done by explicitly comparing canonical representations. I then recommend the use of canonical types that only permit canonical representations.
Definition of Functional Equality
In a functional language, the principle of functional equality says that if a == b, then there should exist no function f for which f(a) != f(b).
Formally:
$$ a = b ⟺ ∀f ~ f(a) = f(b) $$
Why Functional Equality is Important
Here are some cases where strict functional equality tests are needed.
Caching
When implementing a cache, two cache keys should probably not be considered equal unless they are functionally equal. Otherwise the cache can return a value for a different key. This would violate the basic principle of a cache, which should only effect program performance, never behavior. And it’s easy to see how subtle differences in behavior stemming from the hazard of cache hits could cause frustrating bugs.
Debugging
Programmers expect equal inputs to produce equal outputs.
Suppose a programmer has written a program that plots data on charts, placing labels with the numeric value next to each point. She may be encounter a situation where a label sometimes is displayed as “4.0” and sometimes is displayed as “4”. While debugging she is perplexed to find that she gets different outputs for two variables that are equal according to the == operator.
Only after considerable frustration does she realize that the inputs, while passing the == test, are functionally different, because one uses floats and the other integers. She was testing for numerical equality, but what she really wanted was functional equality.
Functional Purity
A functionally pure language must respect the principle of referential transparency. An expression is referentially transparent if it can be replaced with its value without changing the behavior of the program. But shouldn’t we be able to replace any value with an equal value without changing the behavior of the program? Obviously yes. Certain functional programming techniques, such as memoization, require testing for functional equality. And so I would argue that a pure functional programming language must support a concept of functional equality.
Different Representations of the Same Value
Programmers are often tempted to think of two different values as being equal when they are different representations of the same ideal value.
- Two timestamps corresponding to the same moment in time but with different time zones
- Two measurements representing the same length but using different units
- Two different semantically identical Unicode strings (e.g. “ñ” (U+00F1) and “ñ” (U+006E U+0303) )
- Two different lists representing the same set
But it is best to think of each of these cases as involving functionally different values that can be used to represent the same ideal value.
Representations Are Values
Mathematically, when we think of “values”, we think of numbers, or other ideal abstractions such as sets. But in programming, values of variables are data which represent something. In most languages values have a type, and the type is part of the value. And values of different types can behave differently. Thus two representations of the same number using different numeric types can be two functionally different values.
Since these representations themselves are values, it helps to think of an ideal value and its representations as different entities, with a 1-to-many relationship.
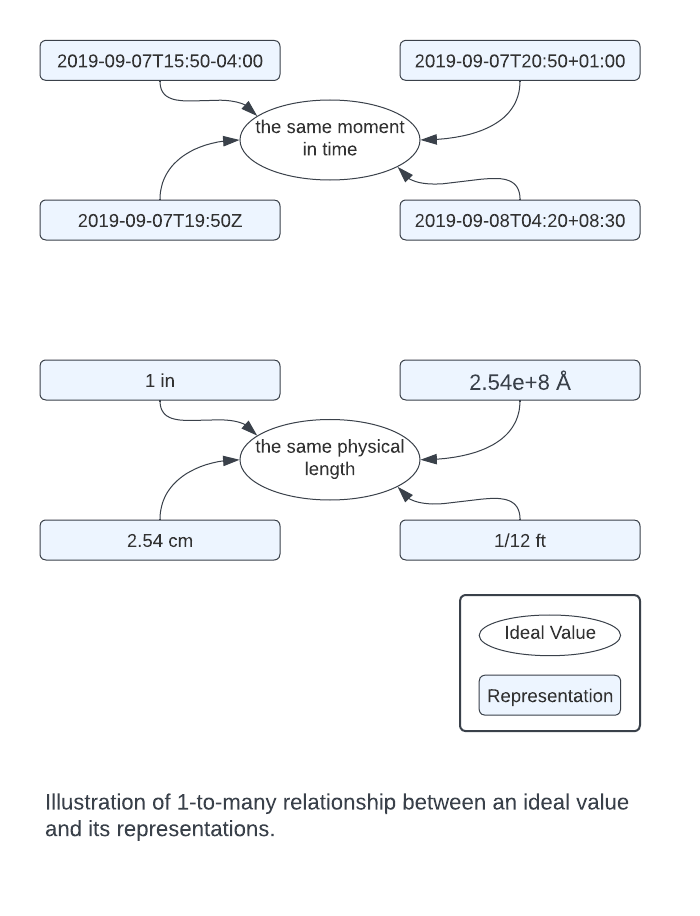
The Representation Problem
Of course, you can’t work with an ideal value without representing it somehow. You need to choose a format for numbers (int64, IEEE float, decimal float, etc.). You need to choose a timestamp when displaying human-readable time zones. You need to store the elements of a set in some order.
But once your language or library allows different possible representations of the same ideal value, you need two different types of equality tests:
- ideal equality (equality of ideal value being represented)
- functional equality (equality of representations)
I call the complexity arising from multiple representations of the same ideal value the representation problem.
Common Solutions to The Representation Problem
There are a few common ways that programming languages try to solve the representation problem.
Implicit Conversion and Special == Logic
In many languages, the == operator implicitly converts numbers to the same type, so that for example an integer variable with value 4 will be == to a float variable with value 4.0 .
And in languages such as Javascript, values of completely different types can sometimes be ==. In Javascript false, 0, "", [], and various other values are all == to false!
Multiple Equality Operators
Implicit conversions and other special logic for cross-type equality comparison effectively converts the == operator into an ideal equality test. But because a functional equality test is important for some applications, these languages must provide some other way to test for functional equality.
For example Javascript provides a separate === operator for strict functional equality.
Disallowing Cross-Type Comparison
In other languages, the == operator is reserved for functional equality.
Ssince values of different types can generally not be functionally equal, == comparisons across types don’t make sense. A float can never == an int.
Since developers could be confused to find that 2+2 != 4.0, in many typed languages, the compiler doesn’t even allow comparison across types. To test for ideal equality, programmers must explicitly convert values to a common type. For example in Go:
var a int64 = 2+2
var b float64 = 4.0
// compile error
// a == b
// true
float64(a) == b== Overloading for Same-Type Comparison
However, this does not completely solve the representation problem, for it’s possible for two functionally different values of the same type to represent the same ideal value. For example in many languages, there is a type that represents a timestamp with a timezone. Two different values can represent the same moment in time in two different time zones.
Two provide an ideal equality test for such types, some languages allows == to be overloaded. But I think this is a mistake, because it robs the type of a functional equality test.
Instead, the language or library should provide some other way of testing for ideal equality.
Canonical Representations
In Go, to test whether two values time.Time represent the same moment in time, you can convert them both to Unix epoch seconds using the Unix() method.
// t1 and t2 are the same time in two different time zones
t1, _ := time.Parse(time.RFC3339, "2016-06-16T19:20:30+00:00")
t2, _ := time.Parse(time.RFC3339, "2016-06-16T12:20:30-07:00")
fmt.Println(t1 == t2)
// Output: false
fmt.Println(t1.Unix() == t2.Unix())
// Output: true
Epoch seconds is a canonical way of representing a moment in time (epoch seconds don’t have time zones, because the number of seconds that have passed since the epoch – January 1, 1970 midnight UTC – is the same no matter where you are on the planet).
Similarly, meters is a canonical way of measuring distance, NFC is a canonical way of representing Unicode strings, etc.
Comparing two values’ canonical representations is more clear and explicit test of ideal equality than special == logic.
Canonical Types
For many applications, you don’t need more than way to represent the ideal value. In such cases, it can be safest to use a canonical type, which is what I call a type that only permits canonical representations.
For example, many databases have separate types for timestamps with and without a timezone. An application that just needs to record when something happens, and not the timezone it happens in, should use a timestamp without a timezone, because this represents a moment in time, stored canonically using epoch seconds. Storing an additional, irrelevant timezone just invites bugs.
I think date/time libraries should also provide separate types for moments in time (e.g. UniversalTime) and timestamps with timezones (e.g. LocalTime). In languages that don’t allow comparison across types, a UniversalTime could not be compared to a LocalTime value, even if the timezone of the LocalTime value happened to be UTC. But LocalTime would have a UniversalTime() method, so to see if two different LocalTime values in two different timezones represented the same actual moment in time, one could compare their UniversalTime values:
localtime1.UniversalTime() == localtime2.UniversalTime()The string form of a UniversalTime (e.g. the value of toString()) would default of course to UTC. UniversalTime would probably be seen to developers as a kind of LocalTime that only supported UTC. Hopefully, developers would recognize that UniversalTime is the proper timestamp type to use for most applications, where timestamps need to be represented in the user’s local timezone only for display purposes.
Other examples of canonical types would be a canonical distance type that only uses meters, a NFC Unicode string type that only allows strings in NFC form, and a canonical set type that stores values in sorted order (so that a function that lists elements of a set behaves equally for equal sets).
Canonical Numbers
But what is the canonical representation of a number? There is a standard scientific notation for writing rational numbers, but this is an arbitrary-length decimal format. This is incompatible with the fixed-length binary format that computer-programs use.
Numeric types have a finite size, because otherwise they tend to grow arbitrarily in size (but not necessarily in magnitude). Further, a precise representation of numbers such as 1/3 as a float would require an infinite amount of memory (0.3333333... and so on forever). Other numeric formats can precisely represent 1/3 but not 1/10, or 2^80. There is no fixed-size canonical format for rational numbers.
However, I think it is still possible to have something like a canonical number type. I hope to discuss this in a future essay.
Summary: Everything is eeeeSame, Everything is Different
If you think about it, any two things are the same in some ways, but different in other ways. So if you want to know whether two values are equal, you must first ask yourself what do you mean by equal?
Two values are functionally equal iff it is never true that f(a) != f(b) for any f.
But often some ideal value can be represented in many different ways. So there is a difference between functional equality tests which compare representations, and ideal equality tests which compare ideal values.
Having more than one way to represent the same ideal value gives rise to the representation problem: the need to support both types of equality tests.
I suggest that languages and libraries solve this problem by reserving the == operator for functional equality, and allow users to test for ideal equality by comparing canonical representations. Using canonical types can be a good way to do this.
